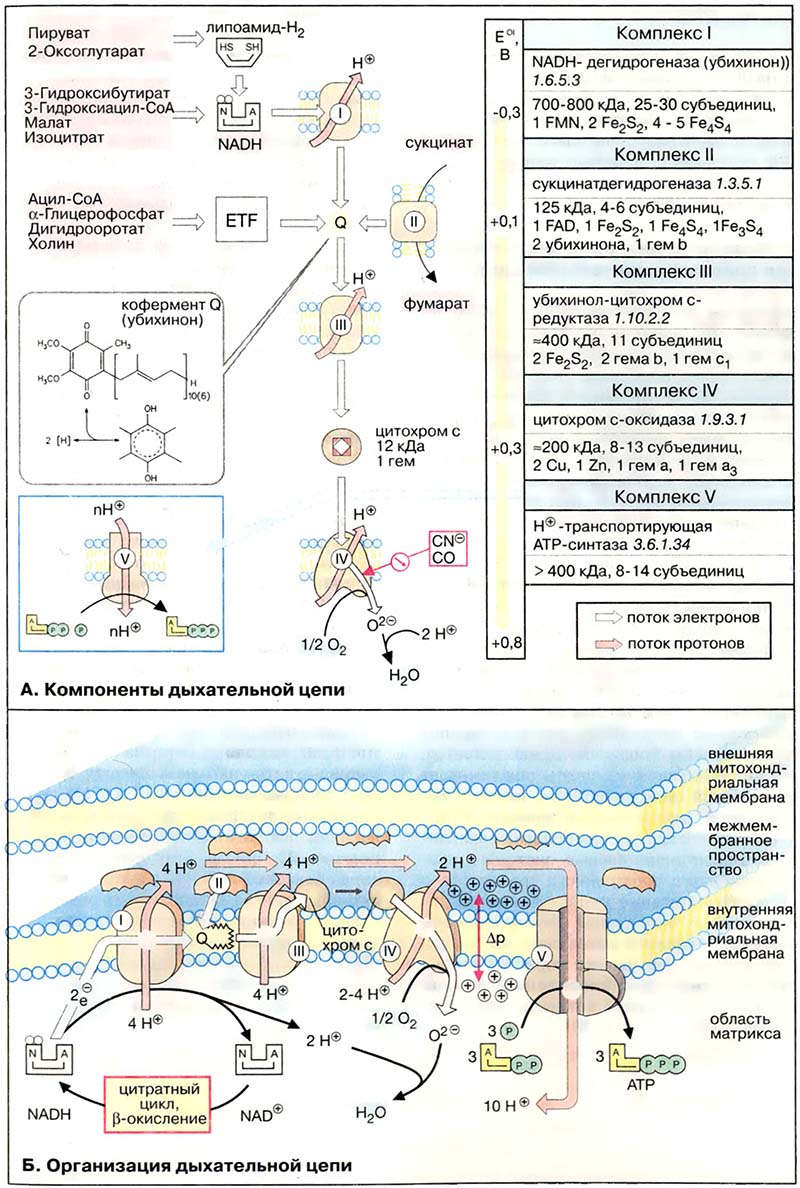
Дыхательная цепь включает три белковых комплекса (комплексы I, III и IV), встроенных во внутреннюю митохондриальную мембрану, и две подвижные молекулы-переносчики — убихинон (кофермент Q) и цитохром c. Сукцинатдегидрогеназа, принадлежащая собственно к цитратному циклу, также может рассматриваться как комплекс II дыхательной цепи. АТФ-синтаза (см. Моноклональные антитела, иммуноанализ) иногда называется комплексом V, хотя она не принимает участия в переносе электронов.
Комплексы дыхательной цепи построены из множества полипептидов и содержат ряд различных окислительно-восстановительных коферментов, связанных с белками (см. Устройство и функционирование эндоплазматического ретикулума и аппарата Гольджи). К ним принадлежат флавин [ФМН (FMN) или ФАД (FAD), в комплексах I и II], железо-серные центры (в I, II и III) и группы гема (в II, III и IV). Детальная структура большинства комплексов ещё не установлена.
Электроны поступают в дыхательную цепь различными путями. При окислении НАДН + Н+ комплекс I переносит электроны через ФМН и Fe/S-центры на убихинон. Образующиеся при окислении сукцината, ацил-КоА и других субстратов электроны переносятся на убихинон комплексом II или другой митохондриальной дегидрогеназой через связанный с ферментом ФАДН2 или флавопротеин (см. Деградация жирных кислот: β-окисление). При этом окисленная форма кофермента Q восстанавливается в ароматический убигидрохинон. Последний переносит электроны в комплекс III, который поставляет их через два гема b, один Fe/S-центр и гем c1 на небольшой гемсодержащий белок цитохром c. Последний переносит электроны к комплексу IV, цитохром c-оксидазе. Цитохром с-оксидаза содержит для осуществления окислительно-восстановительных реакций два медьсодержащих центра (CuA и CuB) и гемы a и a3, через которые электроны, наконец, поступают к кислороду. При восстановлении O2 образуется сильный основной анион O2-, который связывает два протона и переходит в воду. Поток электронов сопряжён с образованным комплексами I, III и IV протонным градиентом.
Комплексы дыхательной цепи построены из множества полипептидов и содержат ряд различных окислительно-восстановительных коферментов, связанных с белками (см. Устройство и функционирование эндоплазматического ретикулума и аппарата Гольджи). К ним принадлежат флавин [ФМН (FMN) или ФАД (FAD), в комплексах I и II], железо-серные центры (в I, II и III) и группы гема (в II, III и IV). Детальная структура большинства комплексов ещё не установлена.
Электроны поступают в дыхательную цепь различными путями. При окислении НАДН + Н+ комплекс I переносит электроны через ФМН и Fe/S-центры на убихинон. Образующиеся при окислении сукцината, ацил-КоА и других субстратов электроны переносятся на убихинон комплексом II или другой митохондриальной дегидрогеназой через связанный с ферментом ФАДН2 или флавопротеин (см. Деградация жирных кислот: β-окисление). При этом окисленная форма кофермента Q восстанавливается в ароматический убигидрохинон. Последний переносит электроны в комплекс III, который поставляет их через два гема b, один Fe/S-центр и гем c1 на небольшой гемсодержащий белок цитохром c. Последний переносит электроны к комплексу IV, цитохром c-оксидазе. Цитохром с-оксидаза содержит для осуществления окислительно-восстановительных реакций два медьсодержащих центра (CuA и CuB) и гемы a и a3, через которые электроны, наконец, поступают к кислороду. При восстановлении O2 образуется сильный основной анион O2-, который связывает два протона и переходит в воду. Поток электронов сопряжён с образованным комплексами I, III и IV протонным градиентом.
Статьи раздела «Дыхательная цепь»:
- Дыхательная цепь
- А. Компоненты дыхательной цепи
- Б. Организация дыхательной цепи
Структура:
Списки:
Сложность материала:
Величины и единицы:
Книги Список книг
Влияние тяжелых металлов на процессы биохимического окисления органических веществ В научной монографии рассмотрены основные направления очистки сточных вод, ...
История биологической химии. Истоки науки Книга посвящена первым шагам взаимодействия химии с биологией и медициной. В ней ...
Защита от биоповреждений, вызываемых грибами Книга посвящена проблеме снижения химической и биологической опасности в сфере ...