Полный математический анализ ферментативной реакции приводит к сложным уравнениям, не пригодным для практического применения. Наиболее удобной оказалась простая модель, разработанная в 1913 году. Она объясняет характерную гиперболическую зависимость активности фермента от концентрации субстрата (1) и позволяет получать константы, которые количественно характеризуют эффективность фермента.
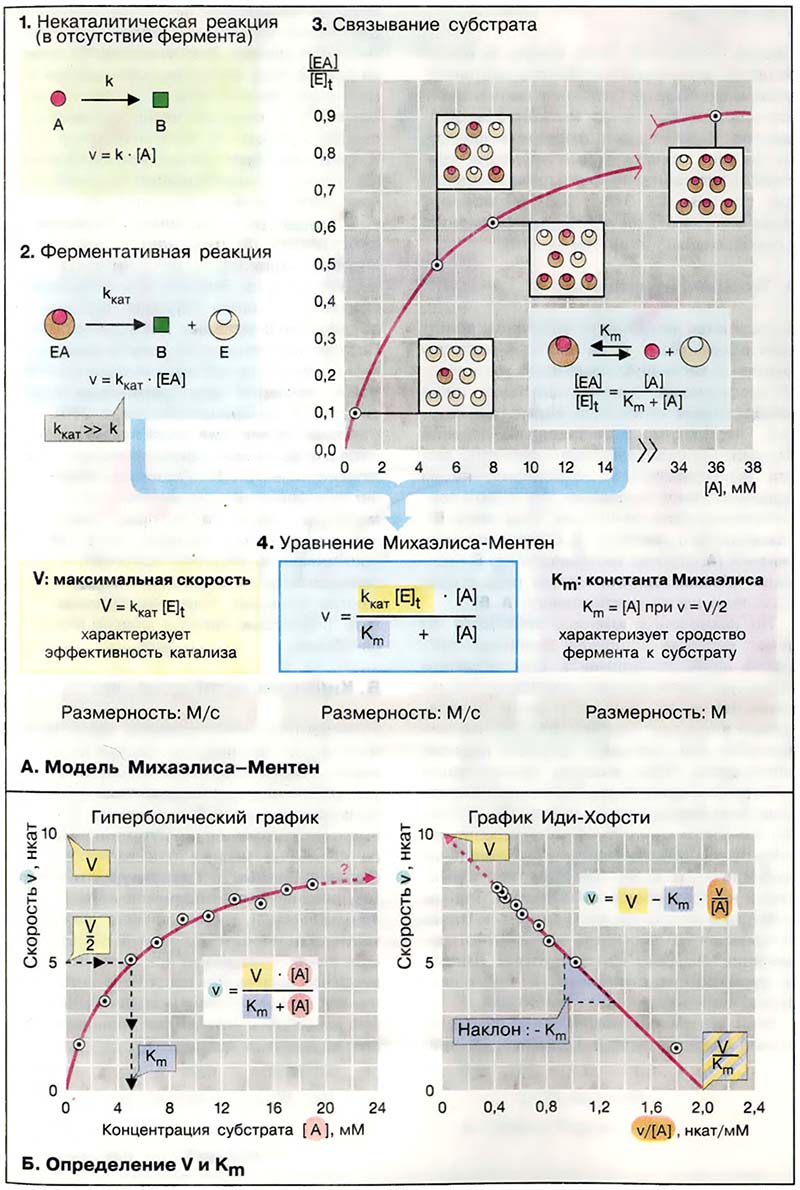
Модель Михаэлиса-Ментен исходит из того, что вначале субстрат A образует с ферментом Е (3) комплекс, который превращается в продукт B намного быстрее, чем в отсутствие фермента. Константа скорости kкат (2) намного выше, чем константа некаталитической реакции k. Константу kкат называют ещё «числом оборотов», поскольку она соответствует числу молекул субстрата, превращаемых в продукт одной молекулой фермента за 1 с. Согласно этой модели, активность фермента определяется долей комплекса ЕА от общей концентрации фермента [E]t, то есть, отношением [ЕА]/[E]t (3). С целью упрощения модель предполагает, что Е, A и ЕА находятся в химическом равновесии согласно закону действующих масс (см. Равновесие), что даёт в итоге для диссоциации комплекса ЕА уравнение:
[Е][А]/[ЕА] = Кm
Поскольку [E]t = [Е] + [ЕА],
[ЕА] = [E]t[A]/(Km + [А])
Из v = kкат[ЕА] (2) и предыдущего выражения получают уравнение Михаэлиса-Ментен (4).
Уравнение содержит две величины (два параметра), которые не зависят от концентрации субстрата [A], но характеризуют свойства фермента: это произведение kкат[Е]t соответствующее максимальной скорости реакции V при высокой концентрации субстрата, и константа Михаэлиса Km, характеризующая сродство фермента к субстрату. Константа Михаэлиса численно равна той концентрации субстрата [A], при которой v достигает половины максимальной величины V (если v = V/2, то [A]/(Km + [A]) = 1/2, то есть Km = [А]). Высокое сродство фермента к субстрату характеризуется низкой величиной Km и наоборот.
Модель Михаэлиса-Ментен основывается на нескольких не совсем реальных допущениях, таких, как необратимое превращение ЕА в Е + B, достижение равновесия между Е, A и ЕА, отсутствие в растворе других форм фермента, кроме Е и ЕА. Только при соблюдении этих гипотетических условий Km соответствует константе диссоциации комплекса, а kкат — константе скорости реакции ЕА → Е + B.
Модель Михаэлиса-Ментен исходит из того, что вначале субстрат A образует с ферментом Е (3) комплекс, который превращается в продукт B намного быстрее, чем в отсутствие фермента. Константа скорости kкат (2) намного выше, чем константа некаталитической реакции k. Константу kкат называют ещё «числом оборотов», поскольку она соответствует числу молекул субстрата, превращаемых в продукт одной молекулой фермента за 1 с. Согласно этой модели, активность фермента определяется долей комплекса ЕА от общей концентрации фермента [E]t, то есть, отношением [ЕА]/[E]t (3). С целью упрощения модель предполагает, что Е, A и ЕА находятся в химическом равновесии согласно закону действующих масс (см. Равновесие), что даёт в итоге для диссоциации комплекса ЕА уравнение:
[Е][А]/[ЕА] = Кm
Поскольку [E]t = [Е] + [ЕА],
[ЕА] = [E]t[A]/(Km + [А])
Из v = kкат[ЕА] (2) и предыдущего выражения получают уравнение Михаэлиса-Ментен (4).
Уравнение содержит две величины (два параметра), которые не зависят от концентрации субстрата [A], но характеризуют свойства фермента: это произведение kкат[Е]t соответствующее максимальной скорости реакции V при высокой концентрации субстрата, и константа Михаэлиса Km, характеризующая сродство фермента к субстрату. Константа Михаэлиса численно равна той концентрации субстрата [A], при которой v достигает половины максимальной величины V (если v = V/2, то [A]/(Km + [A]) = 1/2, то есть Km = [А]). Высокое сродство фермента к субстрату характеризуется низкой величиной Km и наоборот.
Модель Михаэлиса-Ментен основывается на нескольких не совсем реальных допущениях, таких, как необратимое превращение ЕА в Е + B, достижение равновесия между Е, A и ЕА, отсутствие в растворе других форм фермента, кроме Е и ЕА. Только при соблюдении этих гипотетических условий Km соответствует константе диссоциации комплекса, а kкат — константе скорости реакции ЕА → Е + B.
Статьи раздела «Кинетика ферментативных реакций»:
- Кинетика ферментативных реакций
- А. Модель Михаэлиса-Ментен
- Б. Определение V и Km
Структура:
Списки:
Сложность материала:
Величины и единицы:
Книги Список книг
Саморегулируемые волны химических реакций и биологических популяций Монография посвящена математическому моделированию и исследованию нелинейных ...
Молекулярная биология процессов развития Книга представляет собой полную сводку современных знаний о молекулярных ...
NMR Studies of Structural Motifs: Protein Folding and Ligand Binding NMR of Structural Motifs: The agrin G3 domain is critical in development and maintenance of the neuromuscular junction. G3 binds -dystroglycan and ...